| 1 |
|
|
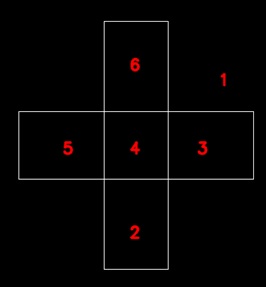
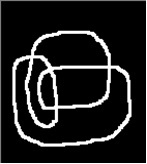
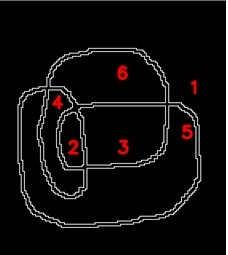
左の左は一筆描き閉路です。線幅は3ピクセルである。その右はその輪郭線である。
輪郭線は番号が付けられサイクルになっている。
この輪郭サイクルはどこも2重になっている。
もし元の描画閉路の幅が限りなく狭ければ、これらの2重のサイクルは重なると考えられる。
元々の閉路は線の交点をグラフの頂点とすると全ての頂点の辺の数は偶数であるので、
それはオイラーグラフであります。
したがって、2重のサイクルセットには2重のオイラーグラフがあると考えられます。
この2重のオイラーグラフは同じ頂点と辺により構成された二つのサイクルセットになります。
しかし、これからできるオイラーサーキットは道筋が違い別のオイラーサーキットになります。
一筆描き閉路に関して
サイクルで囲まれた領域を頂点、サイクルの隣接を辺とするグラフは2分グラフであるので、
2重サイクルのグラフはサイクルの隣接を基準にサイクルを分けることができると考えられます。
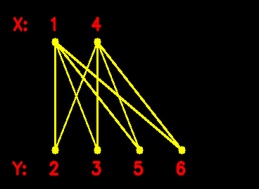
即ちそれは2分グラフのXとYのパーティションになる。
|
| 2 |
|
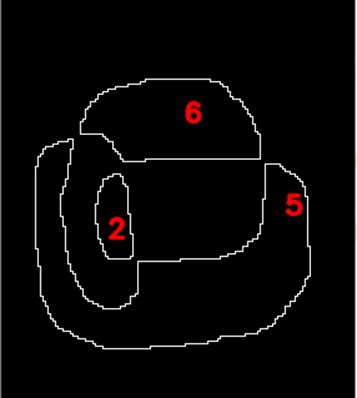
|
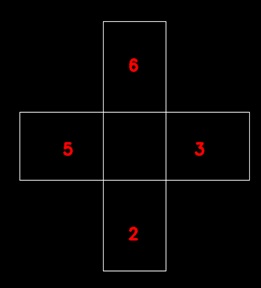
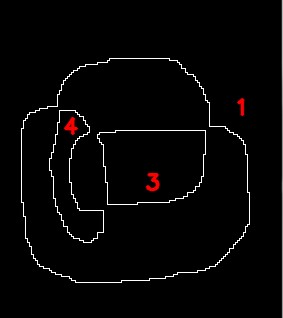
上記のパーティションがこの二つのサイクルセットです。
|
| 3 |
|
|
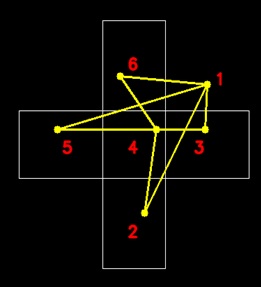
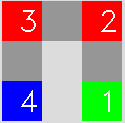
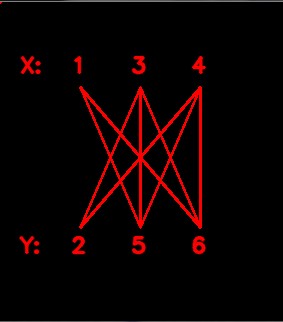
左は全ての隣接をチェックして、2分グラフを描いたものです。
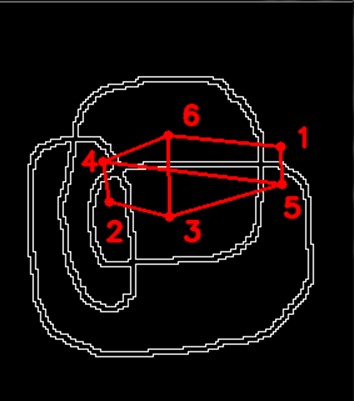
右はサイクルを頂点とする領域とサイクルの隣接を辺とするグラフ(2分グラフ)描いたものです。
|
| 4 |

|

|
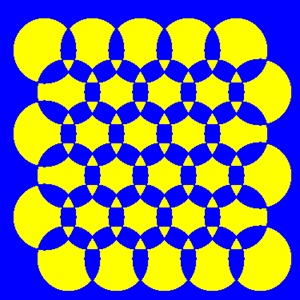
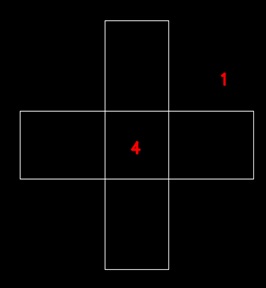
左の左は線幅1ピクセルで描いた閉路です 。
左の右はその輪郭線です。どこも2重になっていますが、ほとんどの場所で重なっているため、1重に見えます。
|
| 5 |

|

|
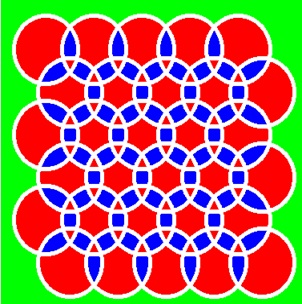
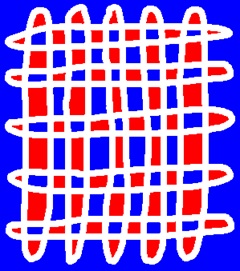
前記の3ピクセルの描画閉路の場合と同じように処理して、2分グラフに分けたものです。
両画像とも同じように見えます。
しかし、二つは違ったサイクルセットになっています。
左は5つのサイクルにより構成され、右は3つのサイクルにより構成されています。
ここで明らかなように、閉じた描画閉路の輪郭線は実質的に2重のオイラーサーキットであるといえます。
|
| 6 |

|

|
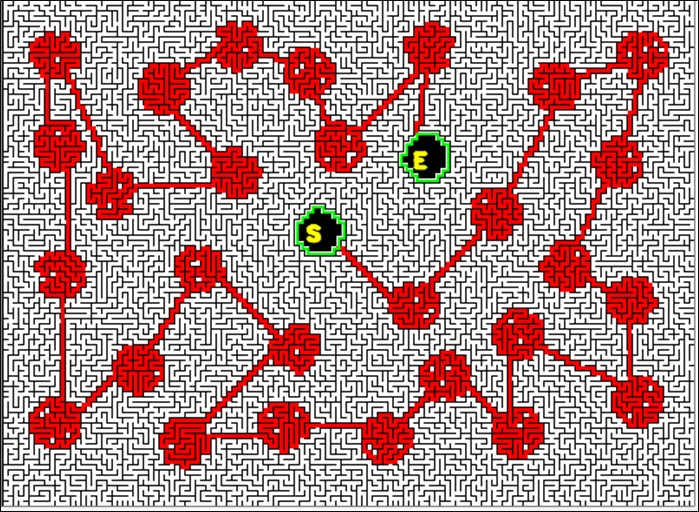
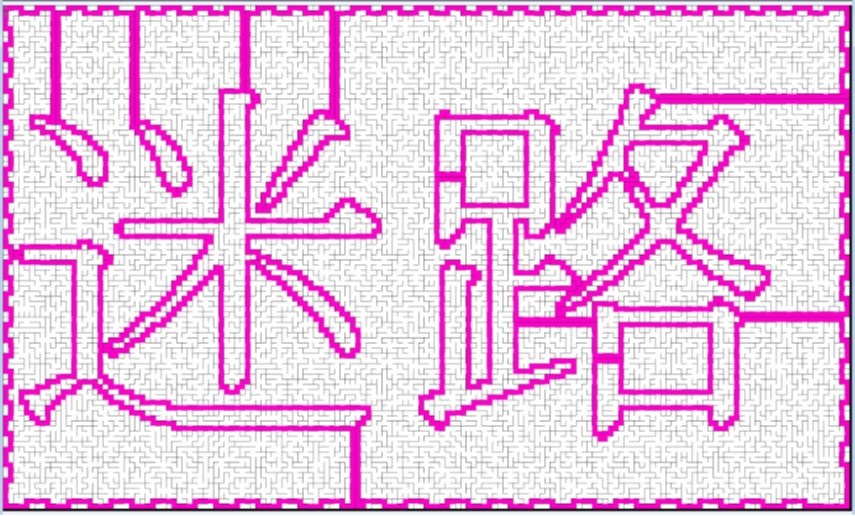
前記のサイクルセット(XもYも)をマージして一つのサイクルに変換し、
適当な位置でパスを切り、スタートとゴールとし、
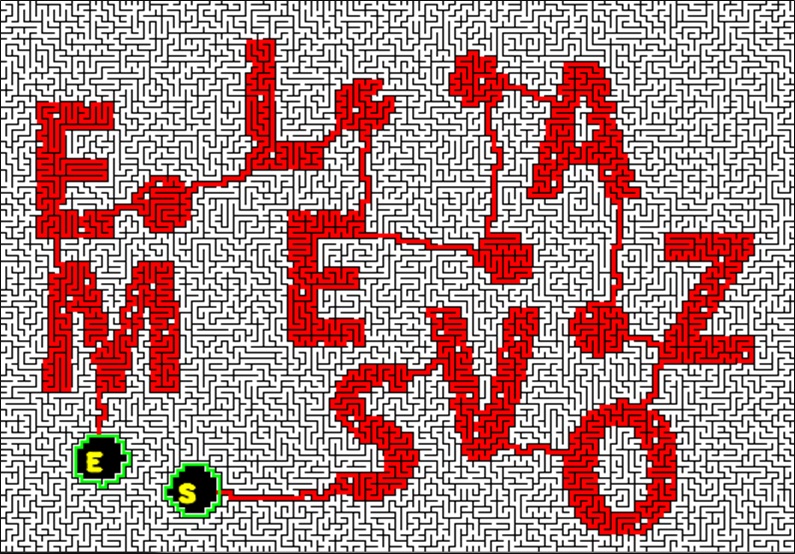
ランダムな袋小路を追加、壁を細く道を太くすると迷路が完成する。
完成した迷路に正解のパスを追加すると図のようになる。
XパートもYパートも同じように見えるが道筋は違う。
|
| 7 |
詳しくは以下のの論文を参照ください。
Tomio Kurokawa, "Maze Construction by Using Characteristics of Eulerian Graphs,"
British Journal of Mathematics & Computer Science, Vol.9, Issue.6, pp.453-472, 2015.6,
SCIENCEDOMAIN international, UK, ISSN: 2231-0851, http://sciencedomain.org/issue/1147
論文のダウンロード-DOI:https://doi.org/10.9734/BJMCS/2015/18125
|